1.5 Método por determinantes

1.5 Método por determinantes

Tenemos que resolver el sistema:

Nuestro sistema de 2*2 lo podemos interpretar como una matriz (2*2) y un vector columna (2*1):

La matriz de 2*2 tiene dos vectores columna: x e y. Al otro vector columna lo llamaremos T

Luego podemos calcular:

= 4*5 - 3*2 = 20 -6 = 14

Para calcular Dx sustituimos en G el vector columna de x por el vector columna de T:

= 22*5 - 3*2 = 110 -54 = 56

Para calcular DY sustituimos en G el vector columna de y por el vector columna de T:

= 4*18 - 22*2 = 72 -44 = 28

Podremos hallar el valor de x efectuando:

Finalmente podremos hallar el valor de y efectuando:

Solución de un sistema de dos ecuaciones lineales con dos incognitas
4x+y+1=0
3x+2y=3


Revisa la siguiente liga para ver el método por determinantes para resolver un sistema de 2 ecuaciones con 2 incógnitas
Solución por Determinantes sistema 2x2

Igualación y determinantes

Ligas de ayuda para ver diferentes métodos de solución

Resolución de sistemas de ecuaciones: sutitición, reducción, gráfico

Ecuaciones simultáneas: ejemplos

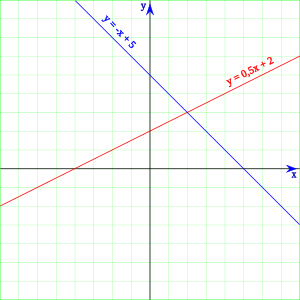Wikipedia Sistema_lineal_de_dos_ecuaciones_con_dos_incognitas

Sistemas de ecuaciones lineales con dos incognitas

http://www.vadenumeros.es/tercero/sistemas-de-ecuaciones.htm

Sistemas de ecuaciones

Solución de un sistema de ecuaciones lineales con dos incógnitas

¡Estoy listo para más retos!

Aplica el método de suma y resta para resolver el sistema:

3x+4y=7

3x+2y=5 En este ejemplo puedes comparar la solución por diferentes métodos

Por suma y resta 3x+4y=7 3x+2y=5 Procedimiento -3x+4y=7 -3x-2y=-5 ---- 2y=2 2y=2 y=2/2 y=1 sustituyendo el valor de "y" en una de las ecuaciones 3x+4y=7 3x+2y=5 3x+4(1)=7 3x+4=7 3x=7-4 3x=3 x=3/3 x=1

Comprobación 3x+4y=7 3x+2y=5 3(1)+4(1)=7 3+4=7 7=7 3(1)+2(1)=5 3+2=5 5=5

Método gráfico